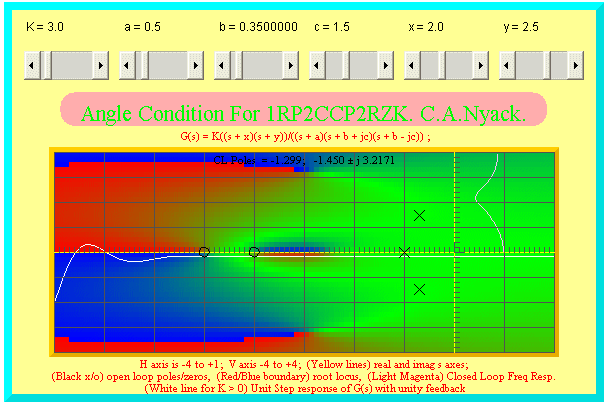
Root Locus for 1 Real Pole, 2 Complex Conjugate Poles and 2 Real Zeros

Cuthbert Nyack

Applet shows the root locus for a system with 1 real pole, 2 cc poles and 2 real zeros. This case has one asymptote at -180°.

For parameters (0.0, 1.0, 1.5, 1.5, 1.5, 2.0) with poles at -1, -1.5 ± j1.5 and zeros at -1.5 and -2, the system is always stable because none of the loci cross the imaginary axis. As K is increased, the step and frequency response both remain fairly flat.

If the zeros are far to the left and the poles are close to the imaginary axis then the system may be unstable for some range of K eg (0.0, 0.05, 0.3, 1.0, 3.8, 3.5). This system is unstable for 0.1 < K < 0.92 and stable for other K's.

If the zeros are close to the imaginary axis and the poles are far to the left eg (0.0, 3.0,2.5, 3.0, 1.0, 0.5) then the step and frequency response is similar to that of a high pass filter.

Gif image showing how applet should appear is shown below.

Return to main page
Return to page index