Phase LagLead 0T1T2 Transient, Frequency Analysis and Root locus

Cuthbert Nyack

Applets below illustrate the application of the LagLead Compensator to a third order Type 1 system. The LagLead compensator can be used for this case when the reduced bandwidth of the Lag compensator may not be acceptable.

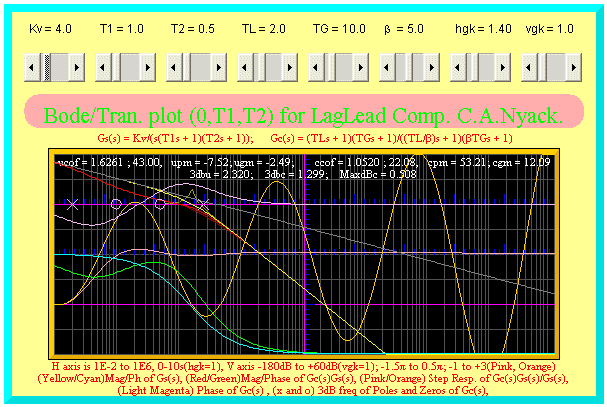
Consider the system Gs(s) shown on the applet with Kv = 4.0, T1 = 1.0 and T2 = 0.5. Depending on the required phase and gain margins some possibilities are indicated below:-

(4.0, 1.0, 0.5, 1.42, 19.0, 5.0, 1.4, 1.0) phm = 60.32°, gm = 15.44dB, dBpeak = 1.156
(4.0, 1.0, 0.5, 2.16, 10.0, 6.0, 1.4, 1.0) phm = 61.27°, gm = 13.61dB, dBpeak = 1.18
(4.0, 1.0, 0.5, 1.32, 17.0, 4.0, 1.4, 1.0) phm = 50.61°, gm = 13.05dB, dBpeak = 1.314
For the parameter values (K, 1.0, 0.5, 2.0, 10.0, 10.0, 1.4, 1.0), the uncompensated system is unstable for K > 3 and the compensated system is unstable for K > ~ 41.8.
For the parameter values (4.0, 1.0, 0.5, 2.0, 10.0, β , 1.4, 1.0), the system is unstable for β > ~ 1.7 and stable for larger β.

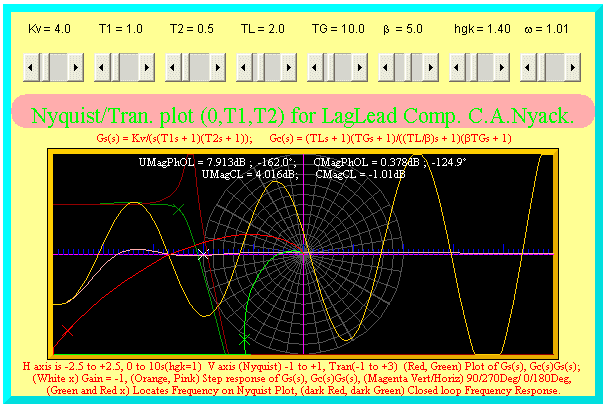
The effect of the LagLead compensator is also shown with the Nyquist plot below. The parameters on the plot show the values of the curves where the "x" is located. The position of the "x" is changed by w on the applet.

UMagPhOL is the uncompensated Open Loop Magnitude and Phase.
CMagPhOL is the compensated Open Loop Magnitude and Phase.
UMagCL is the uncompensated Closed Loop Magnitude.
CMagCL is the compensated Closed Loop Magnitude.

eg parameters (0.0, 1.0, 0.5, 1.5, 2.0, 5.0, 1.4, 3.0) show the general shape of the root locus. With these parameters, the system has poles at 0, -1, and -2 while the compensator has zeros at -0.5, -0.667 and poles at -0.1 and -3.33. with 5 poles and 2 zeros the root locus has 3 asymptotes.
There are 5 starting points for the loci corresponding to the 5 poles. One loci starts at -3.33 and continues along the real axis to -∞. Locus starting at 0 meets loci starting -0.1, move off the real axis, recombine and end up at the 2 zeros at -0.5 and -0.667. Locus starting at -1 meet locus starting at -2, move off the real axis and tends towards the asymptotes at +60° and -60° eventually crossing the imaginary axis at ~±j2.4.

Design by the root locus method means finding values for the compensator parameters which places the dominant closed loop poles at specified locations.

eg parameters (3.0, 1.0, 0.5, 1.44, 18.6, 3.86, 1.4, 2.0) produce dominant closed loop poles at ~ -.64 ± ~j 1.2, the magnitude of the pole is ~ 1.36 and the angle made with the real axis is 62° corresponding to z = ~0.63. With these poles the phase margin is 58.13°, gain margin is 14.41dB, peak closed loop response is 0.366dB, compensated 3dB frequency is 1.099rad/s and the slope at crossover has decreased from 40.08 to 21.34dB/dec.

Gif images below shows how applets should appear.

Return to main page
Return to page index