Non Linear 2nd order system with Cubic.
Cuthbert Nyack
When the controller used in a control system has nonlinear characteristics, then that nonlinearity may be approximated
as a cubic characteristic.
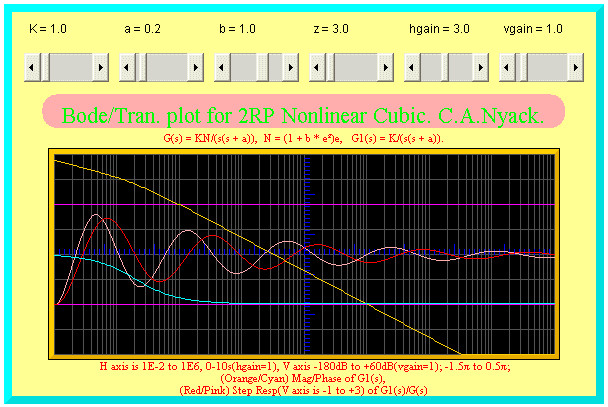
The applets below illustrate the changes in the dynamics of
second order systems when the controller has cubic characteristics.
The extent of the nonlinearity is determined by the parameter b which
can be +ve or -ve.
The applets indicate that the effect of the cubic is to increase or decrease the gain and transient frequency depending on whether b is +ve or -ve. Since a second order system is always stable and the cubic does not affect the phase,
then the cubic nonlinearity does not result in instability of a
second order system. The response does show some modification of the waveform resulting from the introduction of the third harmonic in
the response.
The applet below shows the step(of height A) response of a second order differential
equation with a cubic term known as the Duffing equation.
for the eg parameters (A, 0.2, 0.0, w, ph,
4.0, 1.0)
for A = 0.1 the response freq w is 1.0, ph = -94.
for A = 0.5 the response freq w is 1.08, ph = -95.
for A = 1.0 the response freq w is 1.21, ph = -92.
This shows that the frequency of oscillation depends on the amplitude,
a characteristic on nonlinear systems. The green plot shows that the
frequency of the linear response is independent of amplitude.
Gif image below shows how applet should appear.
Return to main page
Return to page index
COPYRIGHT © 2006 Cuthbert Nyack.

